
La división es una forma simplificada de resta. Es el proceso opuesto a la multiplicación y ha sido definida como la operación a través de la cual, dado el producto de dos números y uno de ellos, se puede encontrar el otro. El número dado se llama dividendo, y el que representa el número de partes en que debe dividirse es el divisor. El resultado entero es el cociente y a la parte sobrante del dividendo cuando la división no es exacta se llama resto.
La división corta es aquella en la que el divisor tiene una única cifra.
Siempre, el dividendo debe colocarse a la izquierda del ábaco dejando una columna libre a la izquierda. El proceso se inicia por la izquierda. Cada división parcial (cuando cada cifra del dividendo se divide entre el divisor) debe hacerse usando los siguientes pasos, como en la división a mano.
Adelantar: consiste en colocar las bolas en la columna adyacente de la izquierda. El numero de bolas colocadas es la parte entera de la división parcial.
Quedar: consiste en colocar tantas bolas a la cifra del dividendo como indique el resto de la división anterior.
Adelantar 0: cuando la cifra del dividendo es menor que el divisor, tal cifra se considera una decena y la siguiente son las unidades, y la división se intenta de nuevo.
Importante: Hay que tener en cuenta que, durante la división, los resultados parciales que aparecen en el ábaco no tienen sentido como cantidad relacionada con la operación. Además, la columna de las decenas del dividendo se convertirá en la columna de las unidades del cociente y cuanto más a la derecha menores seran las particiones de la unidad: décimas, centésimas, milésimas,...
Colocamos el dividendo dejando una columna libre a la izquierda.
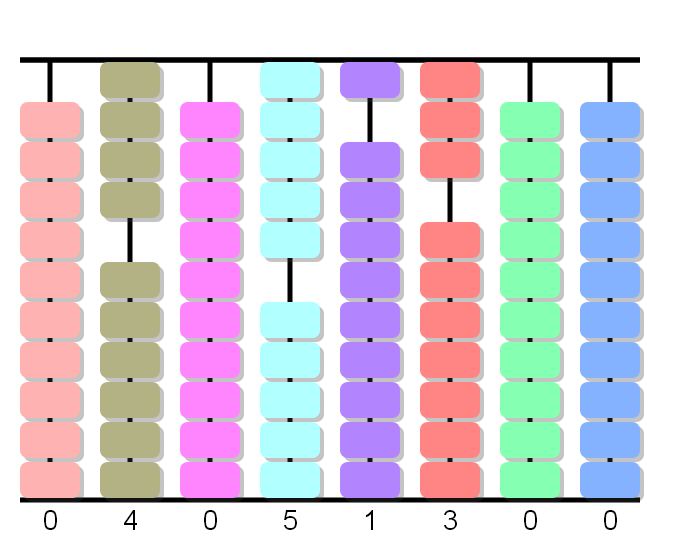
4÷4, adelanta 1 queda 0: marcamos 1 en la primera columna y borramos las de la segunda columna.
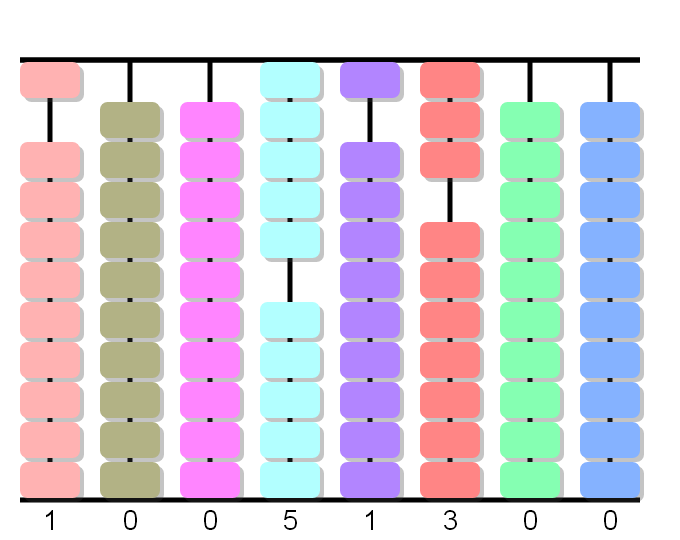
0÷4, adelanta 0 queda 0. A la siguiente división.
5÷4, adelanta 1 queda 1: dejamos una bola en la siguiente columna y otra en la columna de las centenas del dividendo.
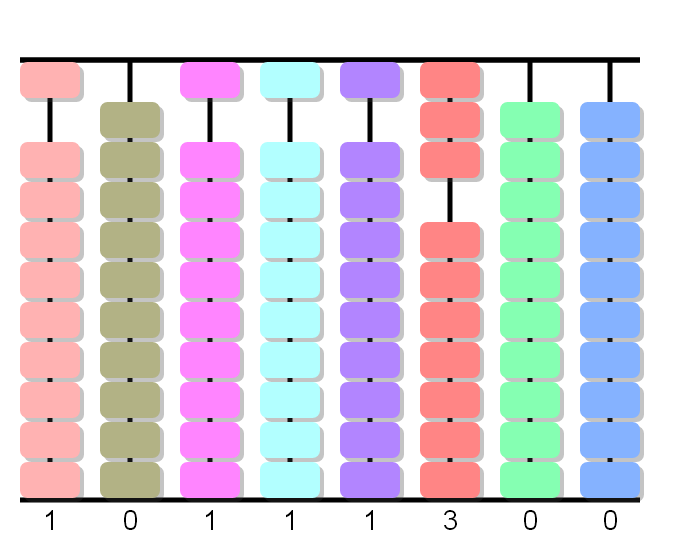
1÷4, adelanta 0 queda 1.
11÷4, adelanta 2 queda 3: ponemos dos bolas en la siguiente columna y tres en la columna de las decenas del dividendo.

3÷4, adelanta 0 queda 3.
33÷4, adelanta 8 queda 1: Cancelamos la unidad, colocamos cuatro bolas en su lugar y dejamos una unidad en la columna de las unidades del dividendo.
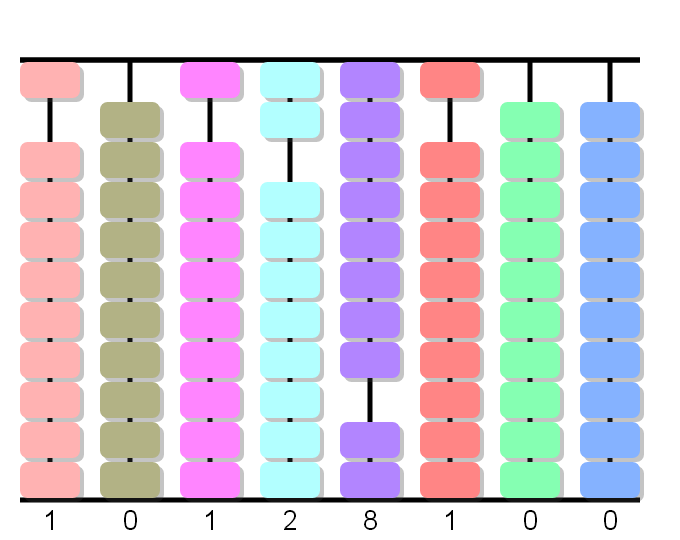
1÷4, adelanta 0 queda 1.
10÷4, adelanta 2 queda 2: Cancelamos la unidad y dejamos dos bolas. Tambien dejamos dos bolas en la columna de las decenas del dividendo.
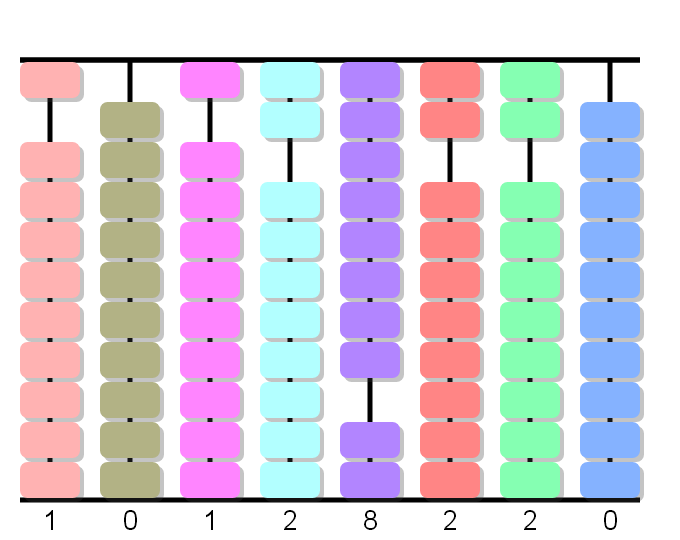
2÷4, adelanta 0 queda 2.
20÷4, adelanta 5: Colocamos cinco bolas en lugar de dos.
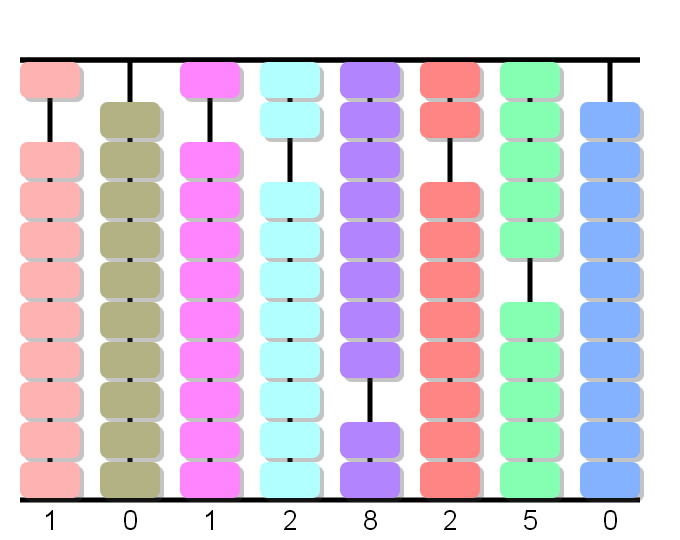
Finalmente el cociente es 10 128,25.
La división larga es aquella en la que el divisor tiene más de una cifra, y el dividendo debe colocarse en el ábaco dejando dos columnas libres a la izquierda.
Los pasos son esencialmente los mismos que en la división corta, pero la división larga conlleva multiplicación: la parte entera de cada división parcial (puesto en el ábaco al adelantar) debe multiplicarse por las cifras del divisor (de izquierda a derecha) y el resultado debe restarse del dividendo. Si esta resta no es posible, e sea, el sustraendo es mayor que el minuendo, el cociente parcial (puesto al adelantar step) debe ser una unidad menor y hacemos la división de nuevo.
Colocamos el dividendo dejando dos columnas libres a la izquierda. El divisor se deja a la derecha con el fin de recordarlo.
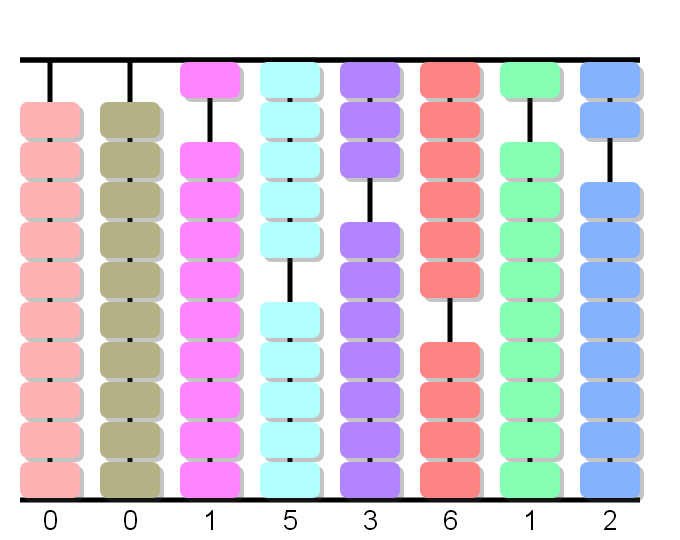
1÷1, adelanta 1: subimos una bola en la primera columna y la multiplicamos por las cifras del cociente, de izquierda a derecha.
1×1 igual a 1. Cancela 1 de 1, obtenemos 0.
1×2 igual a 2. Cancela 2 de 5, obtenemos 3.
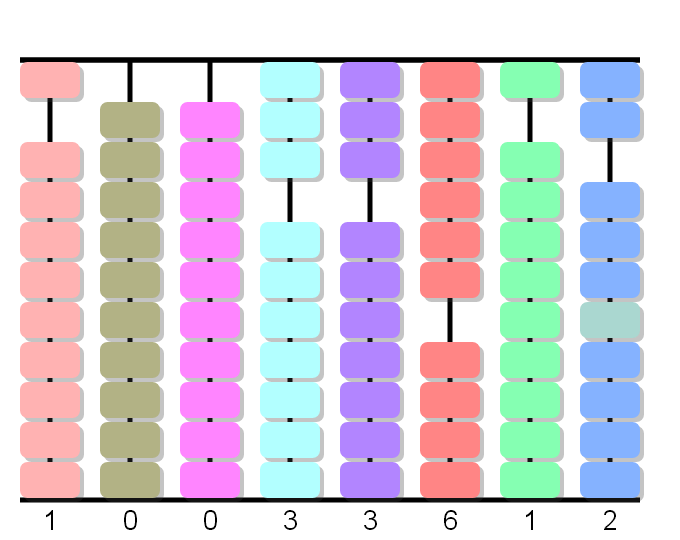
3÷1, adelanta 3: subimos tres bolas en la segunda columna.
3×1 igual a 3. Cancelamos 3 de 3, obtenemos 0.
3×2 igual a 6. Como no es posible cancelar 6 de 3, el cociente parcial es demasiado grande y debe intentarse de nuevo.
3÷1, adelanta 2 (uno menos): subimos dos bolas en la segunda columna.
2×1 igual a 2. Cancelamos 2 de 3, obtenemos 1.
2×2 igual a 4. -4 de 13: Cancela 10, devuelve 6. Obtenemos 9 en la cuarta columna.

9÷1, adelantar 9. En tal caso la resta no es posible. Ahora, 9÷1, adelantar 8 (uno menos): colocamos ocho bolas en la tercera columna.
8×1 igual a 8. Cancelamos 8 de 9, obtenemos 1.
8×2 igual a 16. Cancelamos 16 de 16, obtenemos 0.
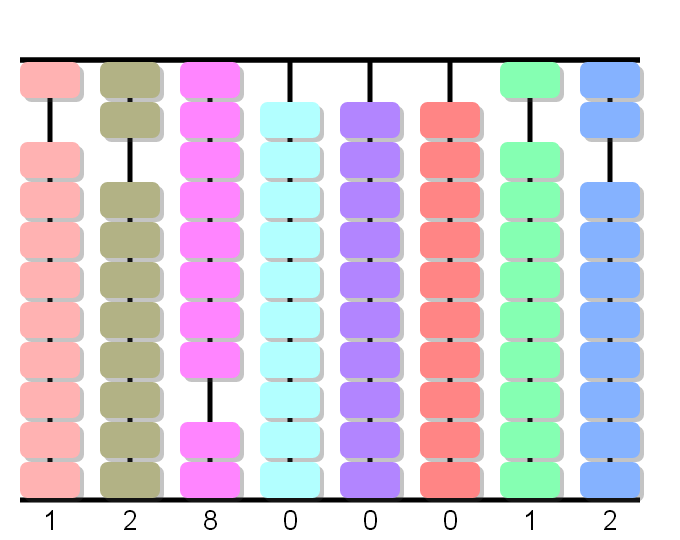
Si cancelamos las bolas del divisor y consideramos que la primera, segunda y tercera columnas son las centenas, decenas y unidades, obtenemos la solución: 128.
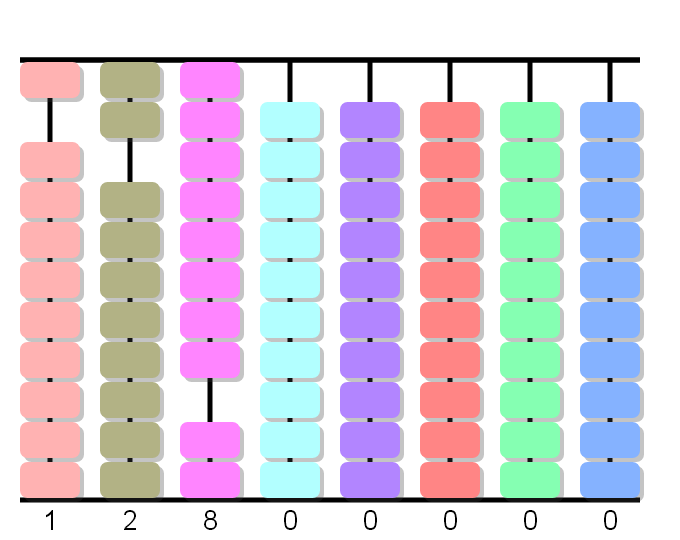
Colocamos el dividendo dejando dos columnas libres a la izquierda.

El dividendo parcial 4 no puede ser dividido entre 5.
46÷5, adelanta 9. Pero en este caso la resta no va a ser posible. Así pues, 46÷5 adelanta 8 y lo colocamos en la primera columna.
8×5 igual a 40. Cancelamos 40 de 46 y obtenemos 6.
8×3 igual a 24. Cancelamos 24 de 61: 6−2 igual a 4; 1−4, cancelamos 10 y devolvemos 6.

37÷5, adelanta 7.
7×5 igual a 35. Cancelamos 35 de 37 y obtenemos 2.
7×3 igual a 21. Cancelamos 21 de 21.
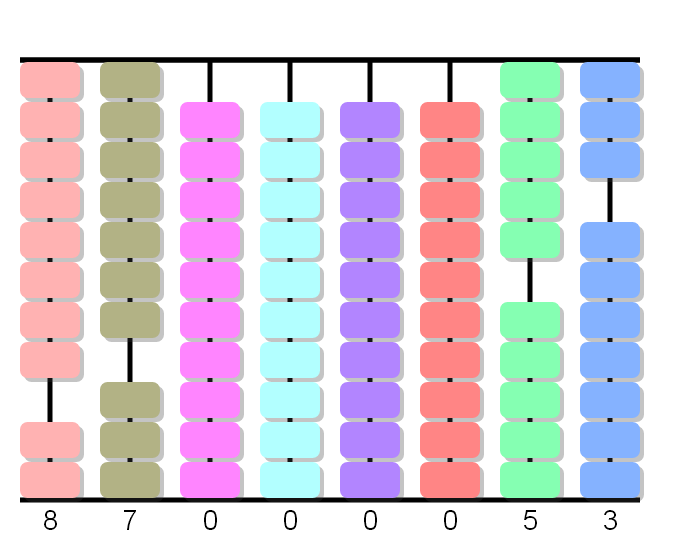
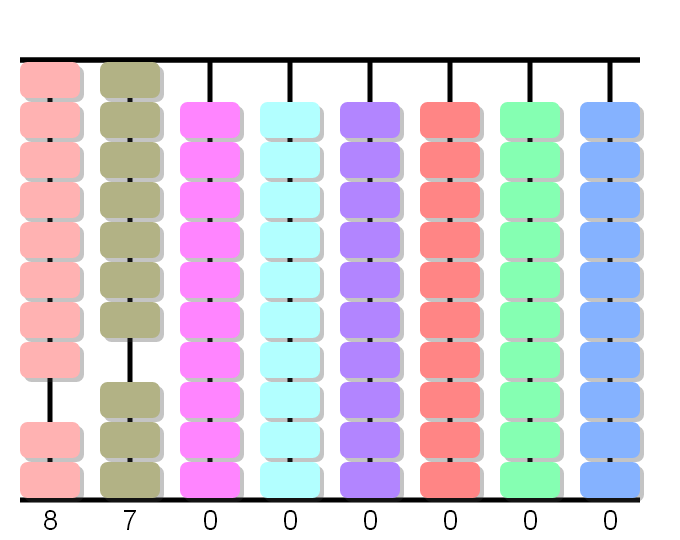
Haga clic en este enlace para practicar la división corta.
Haga clic en este enlace para practicar la división larga.
