
Multiplication is the process of taking one number as many times as there are units in another, or, is a short process of finding the sum of several equal numbers. The multiplicand is the number taken or multiplied; the multiplier is the number that shows how many times the multiplicand is taken; and the product is the result of multiplying.
Since multiplicand and multiplier can change their roles, it is always better to take the greater number as the multiplicand.
The fundamental requisite in this process is to have a masterly knowledge of addition rules and one-figure multiplication.

The multiplicand must be placed leaving one vacant column on the right, because there will be placed the units of the product.
Start multiplying on the right.
The column of the units of the multiplicand will be, after multiplying, the column of the tens of the product, and so on.
Important: It should be noticed during the multiplication that the partial results showed by the abacus have no sense as a quantity related with the operation. They are just a mixure of multiplicand and product: the minimal set of numbers necessary to continue multipliying and to save the definitive figures of the product.
Place the multiplicand 316, on the right-hand side of the frame, leaving one vacant column on the right.
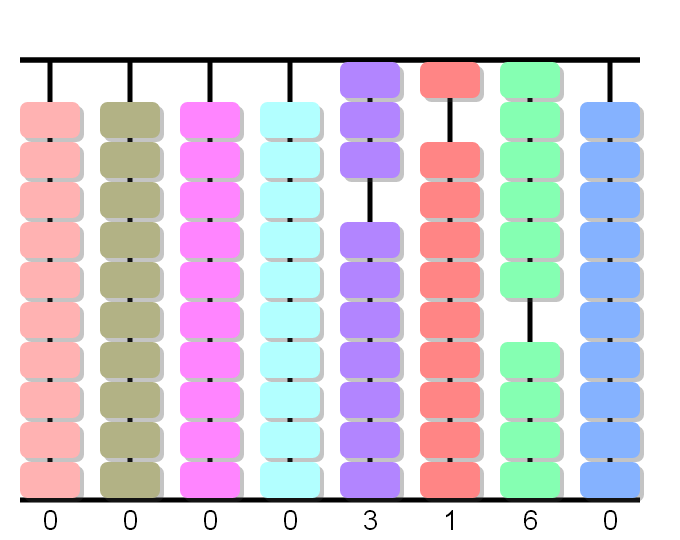
4x6 equals 24. But 24 is composed of 2 tens and 4 units. Therefore the figure 4 is placed in the units' column of the product (next column on the right from the units' place of the multiplicand) and we cancel the units' figure of the multiplicand which is 6 and in its place put the figure 2 (tens of the partial product).
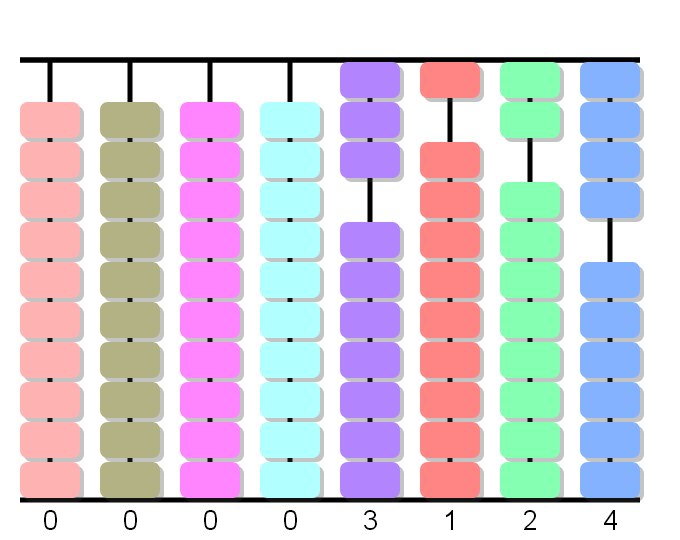
4x1 equals 4. Here the number 4 means 4 tens, the product of 4 times one ten. Therefores the figure 4 is put in the tens' place of the product; i.e. add 4 to the tens of the preceding partial product (2 plus 4 equals 6). The tens' place of the product should now read 6. Immediately cancel the 1 in the tens' place of the multiplicand.
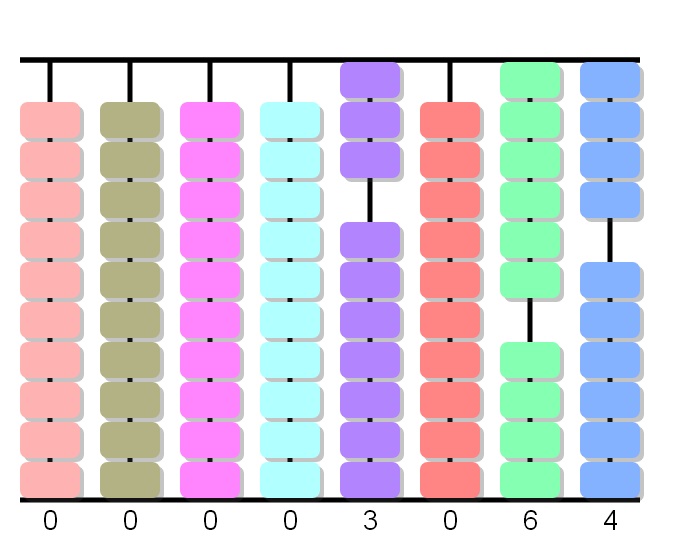
4x3 equals 12. 2 is put in the hundreds' column of the product and the figure multiplied, 3, is cancelled and in its place the figure 1 is put. Hence the product is 1264.
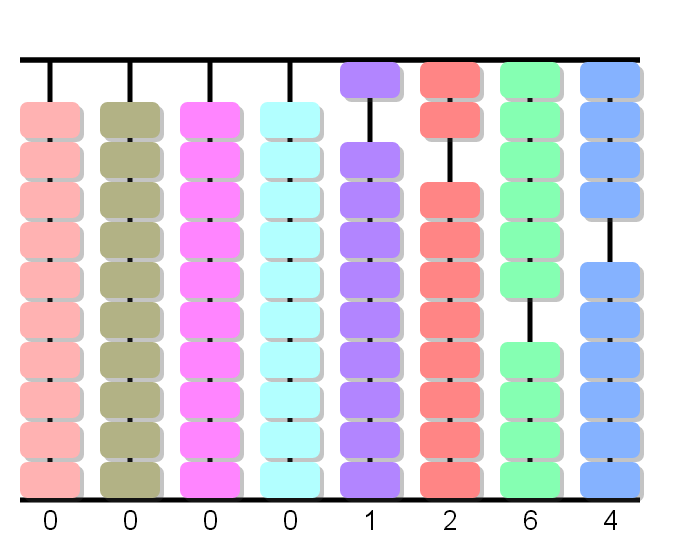
When the multiplier is expressed by more than one figure, for convenience, the multiplier is put near the left-hand side of the abacus so that it can be remembered, and the multiplicand is placed near the right-hand side, leaving for the product as many columns as figures has the multiplier.
Place the multiplicand and the multiplier in the abacus leaving two vacant columns on the right.
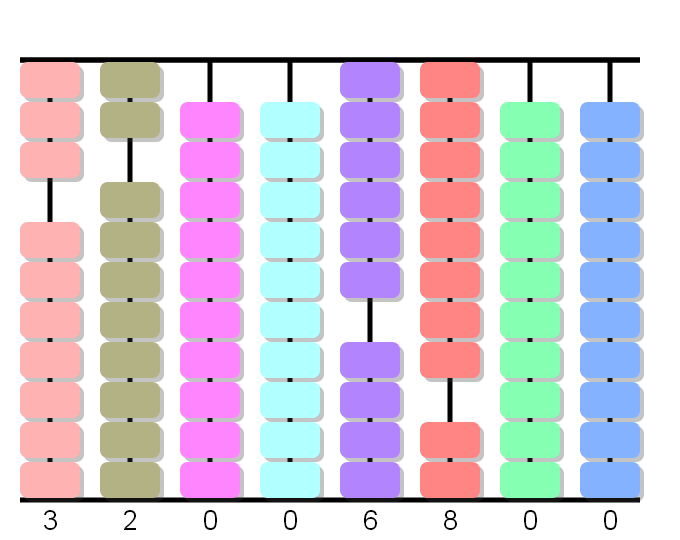
2x8 equals 16. We place 1 in the first column on the right of the multiplicand and 6 in the second column on the right from the figure multiplied, which is 8.
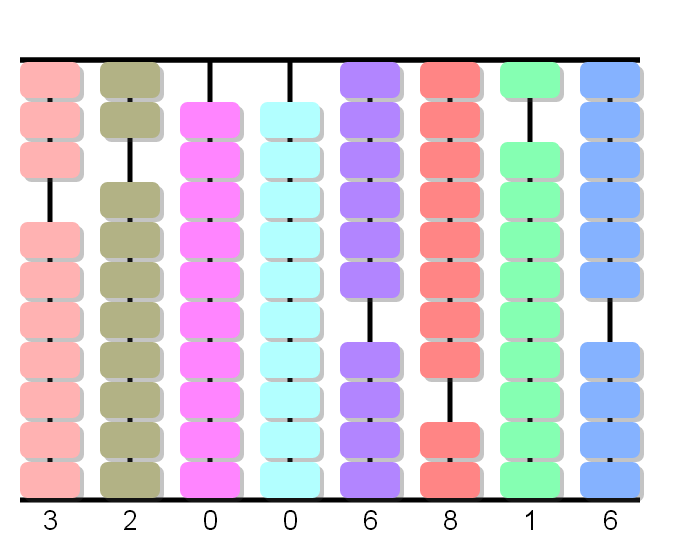
3 x 8 equals 24. We at once cancel the figure multiplied, 8, and in its place put 2 and add 4 in the next column on the right.
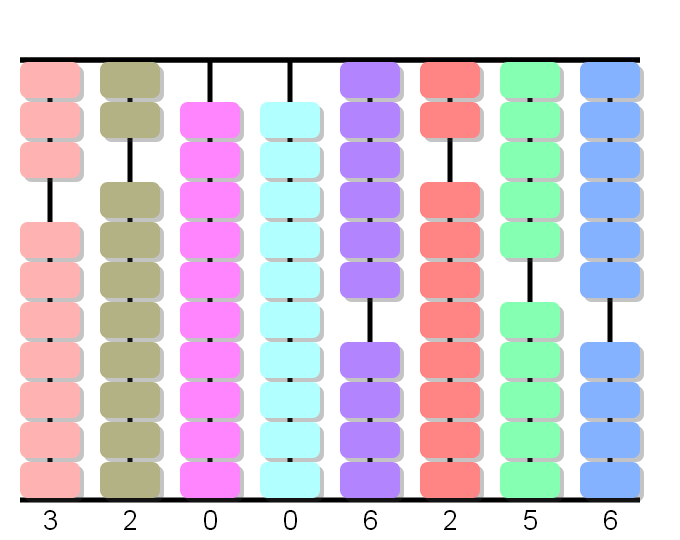
2x6 equals 12. We add 1 on the third column on the right and 2 on the second column.

3 x 6 equals 18. We at once cancel the 6 and put 1 in its place and add 8 in the next column on the right (rule +8: forward 10, cancel 2).
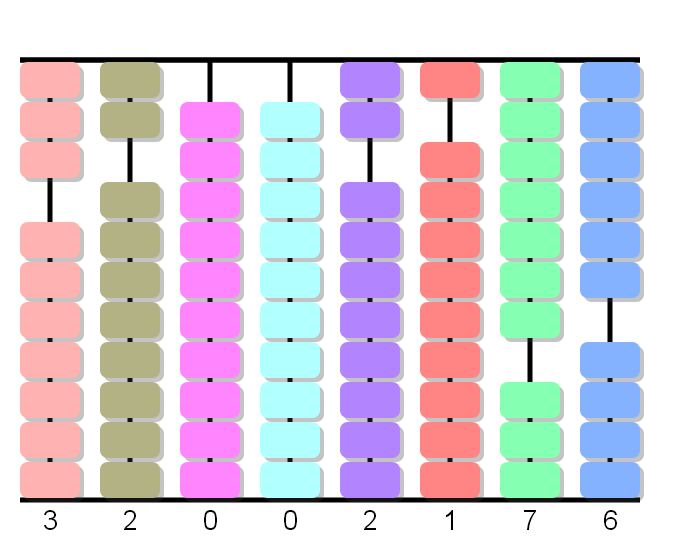
We remove the multiplier from the abacus.
Hence the product is 2176.
Click on this link to practice the one-figure multiplication.
Click on this link to practice the general multiplication.
