
Division is a short form of subtraction. It is the reverse process of multiplication and has been defined as the operation by which, given the product of two numbers and one of them, the other can be found. The given number is called the dividend, and the other number showing into who many equal parts the given number is to be divided is called the divisor. The result of the integer division is the quotient and the part of the dividend left when division is not exact is called the remainder.
Short division is used only when the divisor has one only figure.
Always, the dividend must be placed on the left of the abacus frame leaving one vacant column on the left. The process starts from the left. Each partial division (when each figure of the dividend is divided by the divisor) must be done using the following steps, as used in pen division:
Forward: it consists in placing the beads on the adjacent column on the left. The number of placed beads is the integer result of the partial division.
Remain: it consists in placing as many beads at the dividend figure as the result of the reminder of the above division.
Forward 0: when the figure of the dividend is lower than the divider, such figure is considered as a ten, the next one as a unit, and the division must be tried again.
Important: It should be noticed during the multiplication that the partial results showed by the abacus have no sense as a quantity related with the operation. Also, the column of the tens of the dividend is where the units of the quotient will be placed. More the right we go smaller partitions of the unit we have: tenth, hundredth, thousandth,...
Place the dividend leaving one vacant column on the left.
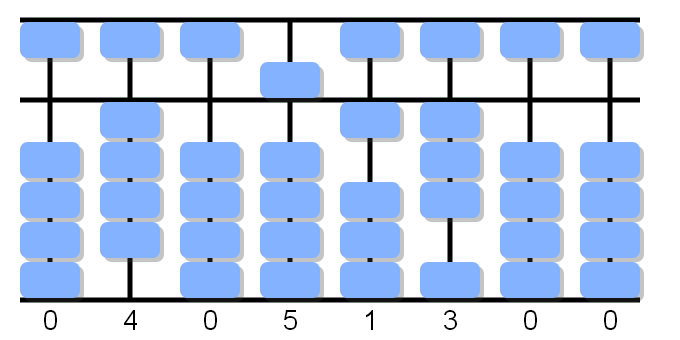
4÷4, forward 1 remain 0: place one bead on the first column and remove the beads of the second column.
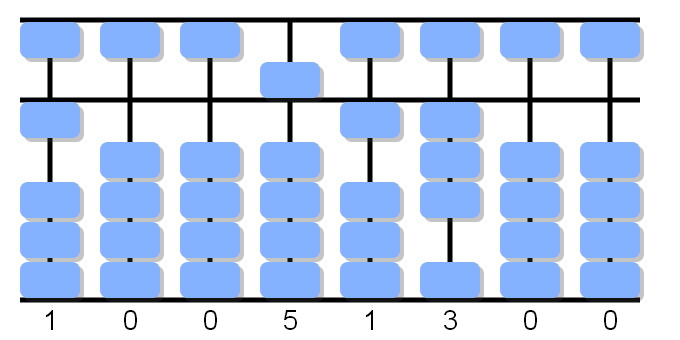
0÷4, forward 0 remain 0. To next partial division.
5÷4, forward 1 remain 1: place one bead on the next column, and place one bead on the hundreds' column of the dividend.

1÷4, forward 0 remain 1.
11÷4, forward 2 remain 3: place two beads on the next column and three beads on the tens' column of the dividend.

3÷4, forward 0 remain 3.
33÷4, forward 8 remain 1: cancel the unit, place four beads instead and place one bead on the units' column of the dividend.

1÷4, forward 0 remain 1.
10÷4, forward 2 remain 2: cancel the unit and place two beads. Also place two beads on the tenths's column of the dividend.

2÷4, forward 0 remain 2.
20÷4, forward 5: Place five beads instead of two.

Hence the quotient is 10 128,25.
Long division is used when the divisor has more than one figure, and the dividend must be placed leaving two vacant columns on the left.
The steps are essentially the same as in short division, but long division involves multiplication: the integer part of each partial division (placed in the abacus when forward) must be multiplied by the figures of the divisor (from left to right) and the result must be substracted from the dividend. If this substraction is not possible, namely the substrahend is greater than the minuend, the partial quotient (placed in forward step) must be one less and the division must be tried again.
Place the dividend leaving two vacant columns on the left. The divisor can be placed on the right in order to remember it.
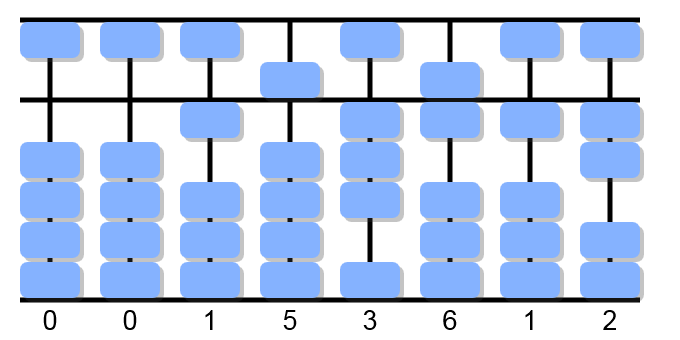
1÷1, forward 1: place one bead on the first column and start multiplying it by the quotient from left to right.
1×1 equals 1. Cancel 1 from 1 and get 0.
1×2 equals 2. Cancel 2 from 5 and get 3.
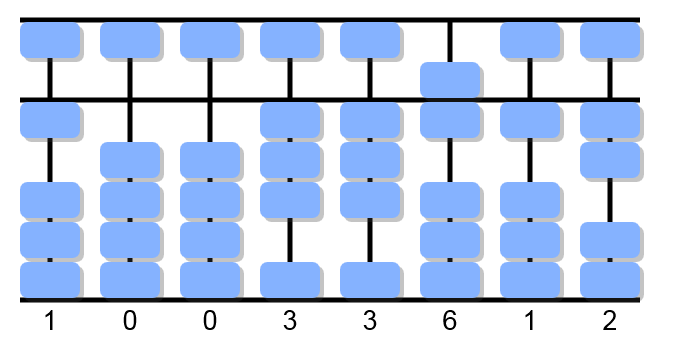
3÷1, forward 3: place tree beads on the second column.
3×1 equals 3. Cancel 3 from 3 and get 0.
3×2 equals 6. Since it is not possible to cancel 6 from 3, the partial quotient is too large and must be tried again.
3÷1, forward 2 (one less): place two beads on the second column.
2×1 equals 2. Cancel 2 from 3 and get 1.
2×2 equals 4. -4 from 13: cancel 10, return 6. We get 9 on the fourth column.
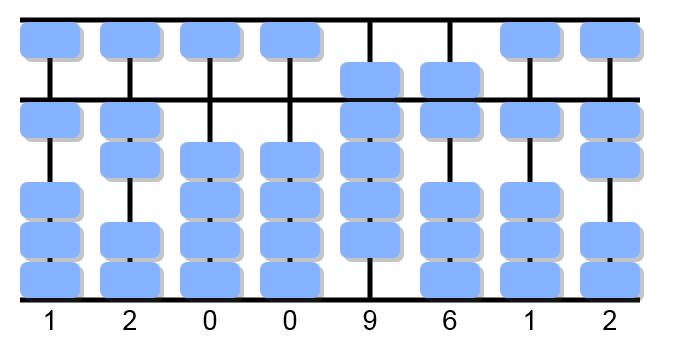
9÷1, forward 9. In this case the substraction will not be possible. So, 9÷1, forward 8 (one less): place eight beads on the third column.
8×1 equals 8. Cancel 8 from 9 and get 1.
8×2 equals 16. Cancel the 16 from 16 and get 0.

If we cancel the beads of de divisor and assume that the first, second and third columns are the hundreds, tens and units we get the solution: 128.
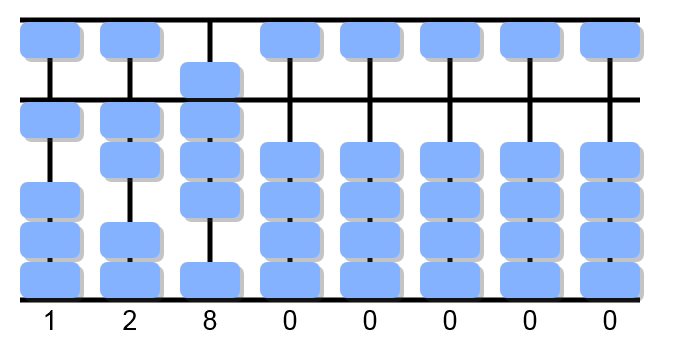
Place the dividend leaving two vacant columns on the left and the divisor on the right.
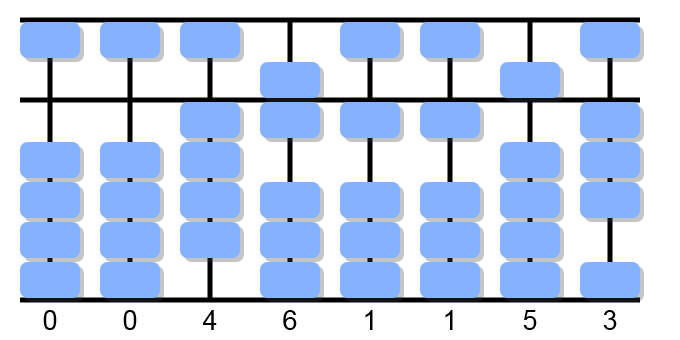
The partial dividend 4 can not be divided by 5.
46÷5, forward 9. But in such case the substraction will not be possible. So, 46÷5 forward 8 and place it on the first column.
8×5 equals 40. Cancel 40 from 46 and get 6.
8×3 equals 24. Cancel 24 from 61: 6−2, cancel 5 and return 3; 1−4, cancel 10 and return 6.

37÷5, forward 7. But in such case the substraction will not be possible. So, 46÷5 forward 8 and place it on the first column.
7×5 equals 35. Cancel 35 from 37 and get 2.
7×3 equals 21. Cancel 21 from 21.
Click on this link to practice short division.
Click on this link to practice long division.